Multiplication

Abstract

Normally we use long multiplication for our manual calculation. However, there are other variance for the Long Multiplication, which can simplify the multiplication for certain situation.

Contents

Before start, here assume a,b,c,d,e,f is single digit decimal number.

For the long multiplication the radix format for the two numeric number (here used 2 digit multiply 2 digit) can be represented by 10ab + 10cd, which identical to (10a+b) * (10c + d), which further turn to 100ac + 100ad + 10bc + bd in the distributed form.

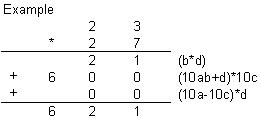
For the variance multiplication, the multiplication for 10ab * 10cd is represent like (b * d) + (((10a + b ) + d ) * 10c) + (10a -10c) * d. which next bd + 100ac + 10bc + 10cd + 10ad – 10cd, and finally become bd + 100ac + 10bc + 10ad. This distributed form which same with long multiplication!!

Example

Simplify Multiplication for certain situation.

The variance multiplication can be simplify the multiplication for certain situation. Example from the first formula we know (b * d) + (((10a + b ) + d ) * 10c) + ((10a -10c) * d), if a equal to c, we can eliminate the last step. Thus (b * d) + (((10a + b ) + d ) * 10c) if a equal c.

That mean 2 steps only, we will get the result.

Reused

Previous example is using 2 digit multiplications, how about 3 digits multiply by 3 digits? By example we use eab*fcd, The formula will like this (b * d) + (((10a + b ) + d ) * 10c) + (10a -10c) * d + ((100e+ 10a + b) + 10c + d) * 100f + ((100e – 100f) * (10c + d)). From this formula we can know, the 3 digits multiplication is sum up the result from the 2 digits multiplication plus the 3 digits part! Thus, we can reuse this result!

Example

Summary

The variance multiplication is applicable to use by decimal number, but this variance also applicable to other system like octal or hexadecimal. Although this multiplication can simplify the multiplication in certain form, but this method will takes long time to calculate for long digit.

Acknowledgements

This method was inspired by my brother Nyuk Kong and sister Nyuk Yung.

Reference

1. http://en.wikipedia.org/wiki/Multiplication_algorithm, Nov 2005